Forecasting war is different to forecasting a coin flip
To properly understand forecasts of future events, we have to remember that we're always learning more about them
This post has a companion notebook, check it out here, or clone the repo here.
Preface: why we use probability to forecast uncertain events
A lot of people, myself included, are excited about using probability to talk about things that are uncertain. Everyone knows we can give probabilities to the results of a coin flip: 50% it lands on heads and 50% it lands on tails. Less widely accepted is the idea that we can give probabilities to any uncertain event, such as whether or not nuclear war will happen in the future. For this example, forecasters on Metaculus offer a probability of 35% (on average) that a nuclear weapon will be detonated in an act of war by 2050. We’ll return to the example of nuclear war later.
I think using probabilities to talk about uncertain events is a great idea. Not everyone agrees. A common alternative to talking about uncertain events using probabilities is to talk about them using verbs. Instead of saying “I think there’s a 35% probability of a nuclear weapon used in war by 2050”, you could say “there might be a nuclear weapon used in war by 2050”.
I think the difference between using probabilities and verbs to talk about uncertain events is a bit like the difference between using centimetres and adjectives to talk about the size of objects. Centimetres are a more precise measure of size, and probabilities are a more precise measure of uncertainty. When I speak precisely, you know what I mean, and you can make calculations based on the information I give you.
To illustrate: if someone is building a house for me and I ring them up to say “I have a two big tables, can you make the dining room big enough to fit them side by side?”, they’re going to struggle to respond. What do I mean when I say a table is big? Are these two big tables the same size? The same shape? On the other hand, if I tell them “I have two tables 100cm x 180cm, can you make the dining room big enough to fit them side by side?”, they’re going to be in a much better position: they know exactly what I mean when I tell them the dimensions, and they can easily add the dimensions to figure out the size of both tables put together, and they can compare this to the planned dimensions of the room. It will take more time for me to get precise measurements of my tables, and I could make a mistake that leads to poor results, but realistically I’m going to be better off measuring my tables than simply describing their size.
Comparing probabilities and verbs is like comparing centimetres and adjectives:
Anyone can understand exactly what I mean if I give them a probability, but not if I given them an verb, just like anyone can understand “100cm”, but not everyone knows what I mean by “big”
It is easier to work out what actions to take on the basis of probabilities than on the basis of adverbs, just as it’s easier to decide if a 100cm table can fit in a room than it is to decide if a “big” table can fit
It is easier to combine multiple probability estimates than to combine adverbs, just as everyone understands that joining two 100cm tables means the result will be 100cm + 100cm across, but no-one knows what results when I join two big tables together
I have to do more work to figure out what probability to tell somebody, just like the fact that measuring is more work than looking at something and saying “it’s big”
I could do a bad job of determining a probability, and I could make an error when I measure something
There is an important difference between probabilities and centimetres: the centimetres we learn about at school are the same as the centimetres we’d use when we’re talking to a builder, but the probabilities we learn about at school are different in an important way to the probabilities we use when we’re making a forecast. That’s what the rest of this post is about.
War forecasts and coin flip forecasts: subjective vs objective probability
The probability we learn about at school is objective probability, but when I give you a forecast I’m using a subjective probability. If I say that the probability of a flipped coin landing on heads is 50%, that is an objective probability. If I say that the probability of a nuclear weapon detonating in an act of war by 2050 is 35%, that is a subjective probability.
There has been an argument going on for over 100 years about whether there’s any fundamental difference between subjective and objective probability, and it shows no sign of ending any time soon. However, there is a simple and important practical difference between the two types of probability:
Objective probabilities do not change when we learn new things
Subjective probabilities do change when we learn new things
We learn about objective probabilities at school: the coin is always 50% to land on heads, and the dice is always 1/6 to land on a 6. No matter what we see the coin or dice actually do, these probabilities never change.
Forecasts are subjective probabilities. As of today (May 28, 2022), Metaculus says there’s a 35% probability for a nuclear weapon to be detonated in war in the next 28 years. Imagine it’s 2072 and no such detonation has happened. It is very likely, I think, that the community will consider such an event to be less than 35% likely in the next 28 year period (that is, by 2100). Perhaps, having seen the continuing absence of nuclear weapons used in war, they might now say there’s just a 15% of such an event between 2072 and 2100 - or perhaps they’d say something different! I don’t know exactly what people will believe then, but it is unlikely to be the same as what we believe today, and if the intervening period is characterised by an absence of nuclear weapon use then I think they will most likely think that nuclear weapon use is less likely than we think today.
Objective probabilities are too inflexible for forecasts
The changeable nature of probabilistic forecasts is an extremely important feature, and one that is not fully understood by some people who are interested in forecasting but aren’t necessarily experts. For example, the graph in this tweet is based (perhaps unknowingly) on the assumption that probabilistic forecasts never change:


The tweet refers to this article, which notes how expert forecasts regarding nuclear war in the next 12 months (experts give it around 1%) seem to imply over 50% probability of nuclear war in the next 100 years.
Both the tweet and the article assume that “the probability of a nuclear war in 12 months” is a number that will not change at all in the next 100 years, no matter what happens in the meantime. Technically, they used an independent and identically distributed (IID) probability model, which is the kind of probability model we learn about at school and is often associated with objective probabilities. The problem with this assumption is that nuclear war forecasts will change when forecasters learn new information. If no nuclear war happens in the next 50 years, then many forecasters will offer a lower annual probability for nuclear war in the remaining 50 years.
Another way of looking at this is that an IID model assumes that forecasters are absolutely certain that in the long run, there will be a nuclear war in exactly 1 out of every 100 years on average. In reality, forecasters are not certain about the rate. They think that there might be fewer nuclear wars than this, or more nuclear wars, and the 1 out of 100 number is their best guess of the rate given what they know right now.
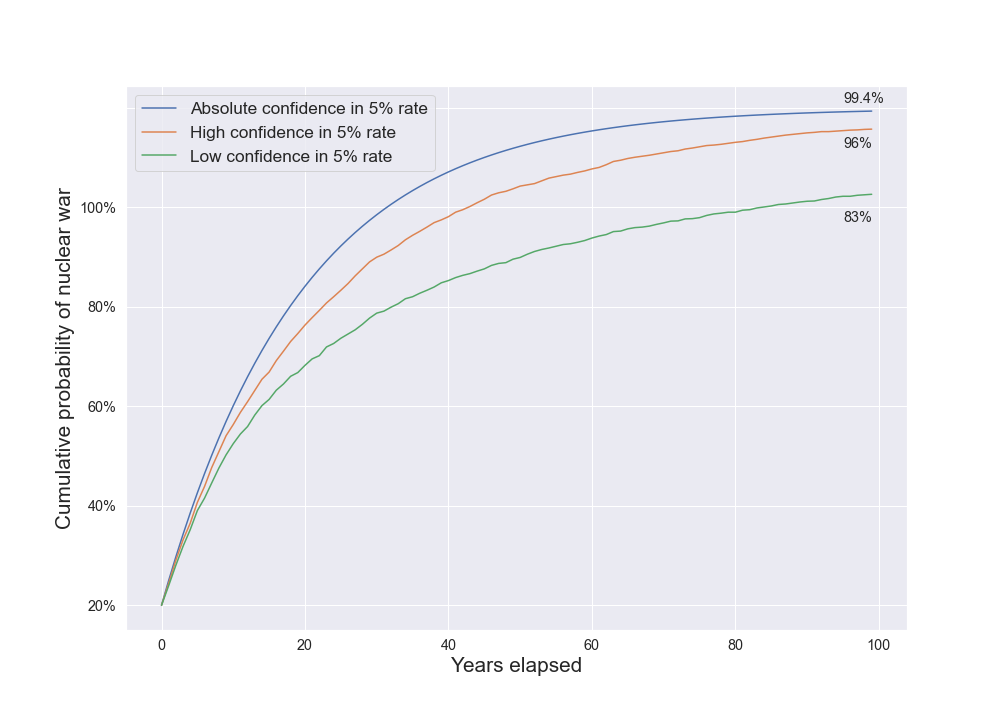
To see the difference, compare an IID model that assigns a 5% probability to nuclear war every year and never changes to models that starts out assigning a 5% annual probability to nuclear war, but updates this downwards after observing years without war:
The IID model regards nuclear war a near certainty after 100 years, giving only a 0.6% chance to avoiding it. A model that is not so confident about the long-run rate of nuclear wars gives a much larger 17% probability of avoiding nuclear war in the next 100 years. The difference is because the lower confidence model, on seeing 40 years with no nuclear war, revises the probability of war in 12 months downward while the IID model continues to assume the chance is 5% each year, whatever it sees along the way. 5% is a very high estimate, and it was chosen to highlight the differences between these different models.
If I use more realistic inputs, an IID model gives a 76% probability in nuclear war in the next 100 years, while a model with lower confidence in the rate gives a 57% probability. The differences are not as large as the contrived example above, but they are still substantial. Note that these inputs are not deeply considered.
The article I linked earlier criticising probabilistic forecasts points out that it is hard to know exactly how rare a rare event is:
This leads to a simple rule: for rare events, it is impossible to make a convincing case that one event is very unlikely (1 in 100.000), but not extremely unlikely (1 in 1.000.000) because, by the nature of rare events, there is not much data to base your estimates off.
This is a big problem for IID models, because they must be absolutely certain about how often the event occurs in the long run. However, this is not such a big problem for more appropriate models such as exchangeable models, introduced below. These models can represent the view that there is some chance the event is 1 in 100 000 rare and some chance that it is 1 in 1 000 000 rare. We should understand that the best guess they can give us for the rarity right now will be higher than the best guess that they will give us after we’ve gone on to see 800 000 years of no events.
It is fine to make a probabilistic forecast without a much data, we just need to be prepared for the fact that the forecast will change when we get more data. People who make use of probabilistic forecasts need to understand this too.
For subjective probabilities, exchangeable models are better than IID models
I’ve argued that we should not interpret probabilistic forecasts like the probabilities that we learn at school (technically speaking, we should not interpret forecasts as IID models). How can we do better? Perhaps the simplest way to improve is to interpret forecasts using exchangeable models instead of IID models. This is what I did to produce the graphs above.
An exchangeable model of nuclear war assumes that, while we don’t know exact level of risk in every year, we do think that the level of risk in each year is the same. This is a simplification too: it seems reasonable to think that we can assess some years to be riskier than others. For example, in years like 2022 in which we know a nuclear armed nation is at war with a neighbour seem riskier than years where we know no such nation is at war. However, even though it is still a simplification, an exchangeable model is a big improvement over an IID model because it allows us to express the fact that right now, we aren’t completely sure of the long run rate, and we expect to change our views as we learn more in the future.
Understanding exchangeable models requires some maths, and in my view the easiest way to use them involves using a probabilistic programming language. I won’t explain either in detail in this article. Instead, if you are interested in learning more, I have created a notebook explaining the maths of exchangeable models, along with an example implementation. You can find the repository on Github if you want to play with it yourself.
I think that probabilistic programming languages are the easiest way to work with probability models. I used numpyro to implement my model, but there are many great alternatives including stan and pymc3. In fact, my model is so simple that you could work it all out using pencil, paper and a calculator (though it might be a bit tedious). However, if you wanted to make things even a little bit more complicated then you would quickly get stuck, while a tool like numpyro can handle many extra complications without requiring you to make much extra effort. If you run into trouble using any of these tools, some great resources are cross validated, as well as the project developers. I would also love to hear if you are trying to implement a probability model and run into trouble.
Conclusion
Forecasts of rates - whether they are annual, weekly or millennial - should not be interpreted in terms of “high school probability” - that is, they should not be interpreted using an IID model. It is much better to use exchangeable models to understand long-term implications of probability estimates; have a look at my notebook for some help getting started in doing this.




Thanks for laying this out. I have seen this objection made before, but hadn't yet seen detailed discussion of good ways to model uncertain cumulative risks.